Reliability and resolution are two independent attributes of a forecast. Reliability is concerned only with the statistical consistency between each class of forecasts F_i and the corresponding distribution of observations O_i that follows such forecasts. Resolution is not affected at all by this consistency.

By contrast, resolution reflects how well different forecast classes can separate cases with different subsequent observed events. Reliability is unaffected by this property of forecast systems.

In principle, reliability can always be statistically 'enforced' or corrected. Unlike reliability, resolution cannot be improved by statistically correcting the forecasts to follow the distribution of ensuing verifying observations.

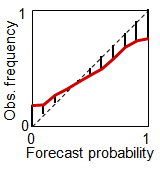
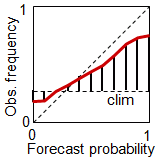
When verifying probabilistic forecasts, quantitative values for reliability and resolution can be generated from the Brier score. The Brier score can be decomposed into three terms and interpreted using the reliability diagram (observed frequency plotted as a function of forecast category). For K probability categories and N samples:

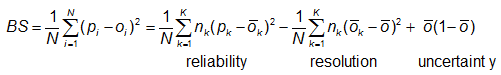
The first term (reliability) measures the weighted error of the reliability curve, where the weights reflect the number of times each probability category is forecasted. It indicates the degree to which forecast probabilities can be taken at face value.	The second term (resolution) measures the distance between the observed relative frequency and climatological frequency. It indicates the degree to which the forecast can separate different situations.	The third term measures the variability of the observations. It indicates the degree to which situations are climatologically easy or difficult to predict. It therefore has nothing to do with forecast quality!

References:

Toth, Z., O. Talagrand, and Y. Zhu, 2006: The attributes of forecast systems. In Predictability of Weather and Climate, ed. T.N. Palmer and R. Hagedorn, Cambridge University Press, 584-595.

Wilks, D.S. 2005: Statistical Methods in the Atmospheric Sciences. 2nd Edition. Elsevier, 627 pp.