NEW APPROACHES TO VERIFYING FORECASTS OF HAZARDOUS WEATHER
Tim Hewson
Met Office, Exeter, U.K.
E-mail: tim.hewson@metoffice.gov.uk
Keywords: verification, hazardous weather, contingency table, deterministic, probabilistic, calibration, THORPEX
1. MOTIVATION
The practice of weather forecasting, particularly for rare events, has historically been hindered by a lack of clear measures of capability. Forecasters will understand that predicting a day with unusually high maxima - such as ‘over 30C at London Heathrow’ - is rather easier than predicting a short, intense rainfall event, such as ‘more than 10mm in 1 hour at Glasgow airport’, but knowledge of exactly how far ahead it is possible to successfully predict such events does not exist. Given the great importance attached, in socio-economic terms, to warning provision, this state of affairs is regrettable. The new ‘deterministic limit’ verification measure introduced here addresses this problem.
2. DEFINITION AND EXAMPLES
We define the deterministic limit (TDL), for a pre-defined, rare meteorological event, to be ‘the lead time (T) at which, over a suitably large and representative forecast sample, number of hits (H) equals the total number of misses and false alarms (X)’ (see Fig. 1a). Null forecasts are ignored, being considered not relevant. The closest counterpart in traditional verification measures is the Critical Success Index (see Jolliffe & Stephenson (2003), Ch 2), which equals H/(H+X). Evidently, at TDL, this is 0.5. What is new here is use of the lead-time dimension.
Choice of CSI=0.5, as opposed to some other value, relates directly to forecast utility. Out of all forecasts, the subset which is concerned with the event in question is made up only of the non-null cases (i.e. H+X). So within this subset forecasts are more likely to be right only for T < TDLT > TDL.
One pre-requisite for defining TDL is that H and X should, respectively, decrease and increase monotonically with T. In practice this should be a characteristic of almost every forecast system, though in cases where small sample size obscures this (e.g. Fig. 1a, top) smoothing could be used. In pure model forecasts assimilation-related spin-up problems could also lead to there being short periods, for small T, when ∂H/∂T > 0. However in systems employing 4D-Var this is less likely to be an issue. In terms of benefits, the deterministic limit:
i) is a simple, meaningful quantity that can be widely understood (by researchers, customers, etc.)
ii) can be applied to a very wide range of forecast parameters
iii) can be used to set appropriate targets for warning provision
iv) can be used to assess changes in performance (of models and/or forecasters)
v) provides guidance on when to switch from deterministic forecasts to probabilistic ones
vi) indicates how much geographical or temporal specificity to build into a forecast, at a given lead
The Lerwick example in Fig. 1a - see caption for full event definition - leads to two conclusions. Firstly, for Force 7 wind predictions, TDL is about 15 hours (marked). For lead times beyond this probabilistic guidance should be used. For Force 8, TDL is less than zero (curves don’t cross), implying that probabilistic guidance should be used for all T. In part the reason TDL is smaller for the more extreme winds is the lower base rate - i.e. the climatology (see caption). Base rate should always be quoted alongside the deterministic limit. In another model example (not shown) with site specific exceedance replaced by exceedance within an area, TDL increases. This is due to reduced specificity - (vi) above - which in turn partly relates to a higher base rate. It is generally accepted that forecasts should be less specific at longer leads - this puts this practice onto a much firmer footing.
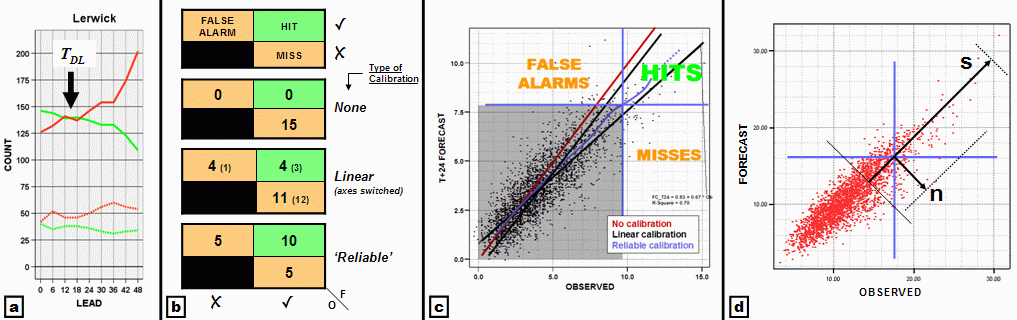
Figure 1: Data for all panels covers a 24 month period from mid 2004, with forecasts provided by the Met Office Mesoscale model (12km resolution). (a): hits (green) and misses + false alarms (red) for mean wind exceedance, at Lerwick, at a fixed time; top lines for ≥ Beaufort Force 7, base rate = 8% (deterministic limit is marked - assumes curves have been smoothed); bottom lines for Force 8, base rate = 2%. (b): 2x2 contingency tables for T+0 North Rona mean wind ≥29 m/s (~Force 11), with differing calibration methods. (c): Scatter plot for Heathrow mean wind forecasts (m/s) for T+24h; lines show calibration methods; 2x2 contingency table structure for ‘Reliable Calibration’ method is overlaid. (d): Scatter plot for Heathrow T+6 wind forecasts (m/s), with method for estimating contingency table characteristics illustrated (see text).
3. CALIBRATION
In analysing strong wind data it became apparent that model bias can significantly impact on TDL. Similar problems would likely be encountered for other parameters, such as rainfall. The clearest way round this is to calibrate model output, by site. Figure 1b illustrates the impact that calibration has on model handling at a very exposed site. Clearly a simple approach, using linear regression, is sub-optimal. The alternative, which we call ‘reliable calibration’, normalises misses to equal false alarms, and in so doing also elevates hits markedly. This method, touched on in Casati et al (2004), is illustrated in Fig. 1c. As the ‘contingency table cross’ (horizontal and vertical lines) moves along the reliable recalibration curve, the number of points in the right half (=event observed) always matches the number in the top half (=event forecast). Note also how the reliable recalibration curve varies through the data range, sometimes lying between the linear regression lines, sometimes outside.
4. FURTHER DISCUSSION
Evidently the structure of a ‘forecast versus observed’ scatter plot (for lead time T) is pivotal for determining whether H > X, which in turn indicates whether TDL > T: tighter point clustering would naturally be consistent with more hits. A simple first order assumption that there is a linear reduction in point density in the orthogonal directions s and n shown on Fig. 1d, above the threshold in question (with ~ zero density reached at the vectors’ ends), leads to the result that TDL ≈ T when s ≈ 3n. This implies that if the cross-calibration spread (s) is more than about one third of the along-calibration spread (n), then event forecasts for that T should in general be probabilistic. This reasoning follows in the spirit of Murphy and Winkler (1987), where the importance of considering the joint distribution of forecasts and observations was highlighted.As Fig 1a illustrates, the error bar on TDL is a function of (∂H/∂T)DL and (∂X/∂T)DL. This can be computed geometrically.
Forecasts of hazardous weather are intrinsically difficult to verify because of low base rates. For the time being this may constrain TDL calculations to focus on thresholds that are less stringent than the ideal. In future we must strive to maximise the verification database by collecting all available data (e.g. 6-hourly maximum wind gusts), by providing model forecasts that are better suited to purpose (e.g. interrogating all model time steps to give 6-hourly maximum gust) and by reserving supercomputer time to perform reruns of new model versions on old cases.
In the context of THORPEX, it is hoped that the deterministic limit concept will assist with long term socio-economic goals, by providing clear guidance on an appropriate structure for warning provision.
REFERENCES
Casati, B., Ross, G. and Stephenson, D.B. 2004. A new intensity-scale approach for the verification of spatial precipitation forecasts. Meteorol. Applications, 11, 141-154.
Jolliffe, I.T. and Stephenson, D.B. (eds), 2003. Forecast Verification: A Practitioner’s Guide in Atmospheric Science. John Wiley & Sons, Chichester U.K. 240 pp.
Murphy, A.H. and Winkler, R.L. 1987: A General Framework for Forecast Verification. Mon. Wea. Rev., 115 , 1330-1338.